05:48
[익명]
수학학과 분들은 어떤 식으로 공부를 해요? 저는 수포자였다가 지금 성인에 한번 수학공부를 다시 해보고 있는데, 예를
저는 수포자였다가 지금 성인에 한번 수학공부를 다시 해보고 있는데, 예를 들면 지금 곱셈역원같은 것에 대해서 알아보고 있어요.예를 들어5/4 나누기 2면은,2가 2/1이 될 수 있다는 것은 알지만,나누기 2/1이 곱하기 1/2가 어떻게 될 수 있는지는 모르겠어요.이런 것을 그냥 그런거야, 하고 받아들이면 되는건가요?아니면 저게 원래 수학 선조들에 의해 정리되었고, 알지만, 그 원리에 도달하기에는 원래 어려운 건가요?벌써부터 막히니 정말 이래도 되나 싶더라구요.다른 여러 수학적 공식들도 있을텐데, 수학과 분들은 이런 공식들이 왜 어떻게 이렇게 되었는지 그런 걸 쉽게 알 수 있는거예요?
어느 초등수학 가르치시는 분이 쓴 글을 보니
다음과 같은 과정을 거치더군요
5/4 ÷ 2/1
= 5×1 / 4×1 ÷ 2×4 / 1×4 .............분모를 일치시키는 통분과정이라고 하더군요
= 5×1 / 2×4..........................위에서 여기 내려오는게 핵심인 것 같은데 분모끼리 같으니 분자끼리 구성된다는 의미인듯
= 5×1 / 4×2
= (5/4) × (1/2)
아마도 이게 나눗셈이 역수의 곱셈이라고 처음 배울때 나오는 과정인 듯 합니다.
(그 글 저자분이 초등수학선생님이셔서)
저는 곱셈의 역원 개념으로 생각하고 있는데
즉, (5/4)÷2 = x라고 하면
(5/4) = x × 2이고
양변에 ×2를 없애려면 곱셈의역원인 1/2를 곱해야 해서
(5/4)×(1/2) = x라고 이해하는데
뭐 딱히 새로울 것은 없어보이네요...
회원가입 혹은 광고 [X]를 누르면 내용이 보입니다
-
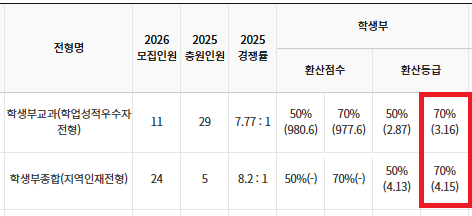
창원대 수시 .. 창원대를 목표로 하고 있는 09년생입니다 지금 제 내신이 5등급제 기준으로
2025.12.01 -

아이폰 16, 16프로 케이스 호환 가능한가요? 16을 쓰고 있는데 일반형은 케이스가 많이 없고 프로형은 많아서
2025.12.01 -

임영웅 11월 브랜드평판 순위 알고싶어요 임영웅 11월 브랜드평판에서 스타부문에서의 임영웅 순위 알고싶어요
2025.11.30 -

전주 고등학교 다자녀 제가 2027학년도 고등학교 입학생인데요 지망하는 학교가 전주 한일고인데 1. 다자녀
2025.11.30 -
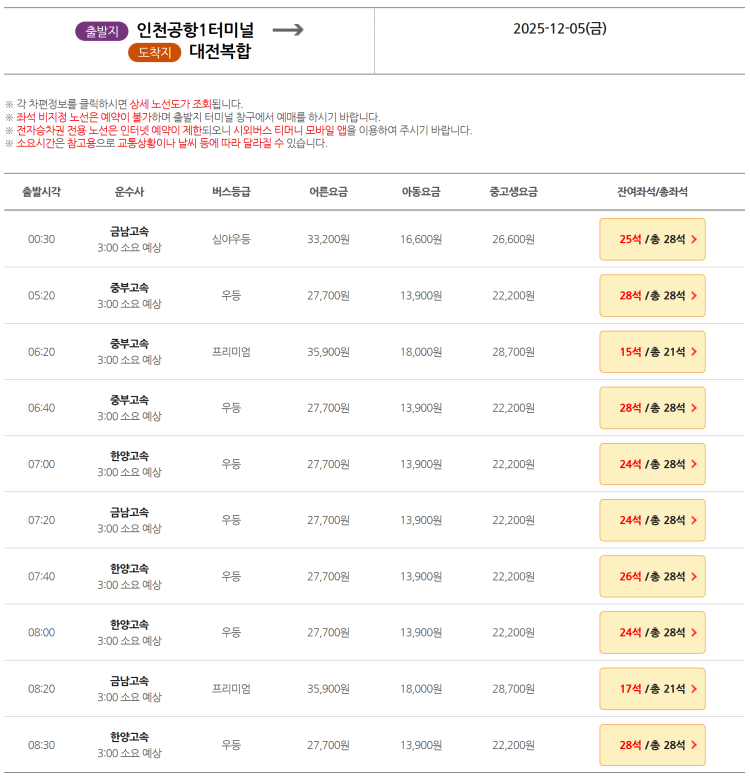
고속버스 예매 인천공항에서 대전으로 가는 버스를 이용하려하는데 버스 노선이 인천공항 2터미널에서 출발해
2025.11.30 -

어떤 야구선수 싸인일까요? 제가 옛날에 롯데 자이언츠 선수한테 싸인받은 싸인볼을 오늘 찾았네요. 어떤
2025.11.29
